This lesson will learn you something about the two's complement. This is a way of representing negative numbers in a byte or in several bytes.
How it works |
Changing the sign |
Math instructions and 2-complement |
Overflow
How it works
Let's take a look at a byte. According to the maximum number of combinations, you can store numbers from 0 to 255 in it.
When you want to use negative numbers, a byte simply stores -128 to 127, where -1 is the same as 255, -2 is 254, -3 is 253, etc...
Now you will probably think : why -128 to 127 and not -127 to 128 ? To find an answer to this question, we need to take a look at the binary notation of the numbers.
We start with -127 to 127. We leave the sign of 128 open for now. We notice that all numbers from -1 to -127 have bit 7 set and that all numbers from 1 to 127 have bit 8 reset. This characteristic can be used to check if a number is positive or negative.
Let's take a look at 128 now, it's %10000000 in binary notation, which means bit 7 is set. And this is why we consider it -128 in the two's complement notation, to be able to use bit 7 to check if a number is negative or positive.
With this system, all binary numbers from 10000000 ($80) to 11111111 ($FF) can contain both positive or negative numbers. You will have to decide if you're going to work with signed or unsigned numbers before you start.
The Z-80 has 2 flags which tell you if the result of an operation is positive or negative. Bit 7 of the flag register, the S flag, will contain bit 7 of the result. It will be set if the sign of the result is minus (M) or reset if the sign is plus (P).
Changing the sign
Changing the sign of a signed byte is not as simple as changing bit 7.
Changing the sign can be done in two ways :
You can subtract it from $100 (or binary : 0000 0001 0000 0000)
You can complement it and count 1 up, -A=NOT(A)+1
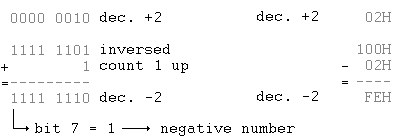
The Z-80 has an easy instruction to change the sign : NEG. It takes 2 bytes and changes the sign of the accumulator
Math instructions and signed numbers
How strange it may sound at first, it is possible to do math instructions with signed numbers (some problems with the division, but for the rest, everything is fine).
When you don't work with signed numbers and you added 1 to 255, the result was zero and the zero flag was set. In the 2-complement 255 is -1, so -1+1=0 !
Adding - Subtracting - Multiplying
No problems here, check it out yourself, everything should work (except when the result is out of the range -128/127 of course - see OverFlow)
Dividing
Dividing signed numbers can give wrong results. A rather simple solution will solve this.
Before dividing, the signs of the numbers are saved somewhere.
Both numbers are made positive and the division is performed
According to the signs of the numbers before dividing, the result is made negative or left alone.
Overflow
An overflow will occur if you try to add 2 numbers with the same sign or when you subtract two numbers with a different sign and the result is either bigger than 127 or smaller than -128.
+121 0111 1001 -106 1001 0110
+100 0110 0100 - 88 1010 1000
---- + --------- + ---- - --------- +
221 1101 1101 (=-35!) -194 (1)0011 1110 (=+62)
|
Note that a carry when using signed numbers does not necessary mean that the result is wrong! Take a look at the following example.
-10 1111 0110
-12 1111 0100
---- + --------- +
-22 (1)1110 1010 (=-22!)
|
Overflow means that the sign needs to be changed. An overflow happens in 2 possible cases :
there is a carry between bit 6 and bit 7, but no carry between bit 7 and the carry bit
there is no carry between bit 6 and bit 7, but there is one between bit 7 and the carry bit
You don't need to check all these carrys yourself, because the Z-80 has a special flag for Overflows : the P/O (parity/overflow) flag. As you can see, the flag is used for two things. First off all, it acts as a parity flag after logical instructions, shifting instructions and rotating instructions. Next to that, it is used to indicate an overflow when using math instructions.
Because there is only one set of mnemonics, you have to use PE(parity even) and PO(parity odd) with conditional jumps even when checking for an overflow. PE indicates an overflow and PO indicates no overflow.
A little example routine that adds to numbers and gives a message with an overflow (Ash/Crash example):
ADD A,B ; add a and b
JP PE,ShowMessage ; jump if overflow
RET
ShowMessage:
LD HL,$0000
LD (CURSOR_POS),HL ; cursor position to top left of screen
LD HL,MsgOverflow
ROM_CALL(D_ZT_STR) ; write string on screen
RET ; return to caller
MsgOverflow:
.db "Overflow !",0
|
Previous lesson |
Contents |
Next lesson