Most processors only understand binary information. This is data composed of only ones and zeros. Where our decimal system has a base of 10, the binary system has a base of 2.

So, when you would count in binary, it would go like 0, 1, 10, 11, 100, 101, 110,...

A '1' or a '0' is called a bit. If you combine 4 bits, e.g. '1100' or '0101', you get a nibble. 8 bits or 2 nibbles makes a byte. Most information will be given in bytes (or words : 2 bytes).

Unsigned
Name	Min value	Max value
Bit	0 (0 dec)	1 (1 dec)
Nibble	0000 (0 dec)	1111 (15 dec)
Byte	0000 0000 (0 dec)	1111 1111 (255 dec)
Word	0000 0000 0000 0000 (0 dec)	1111 1111 1111 1111 (65535 dec)

As you can see, you can only store positive numbers. But when you really need to work with negative numbers, you could see the MSB (Most Significant bit - bit that is the furthest to the left - bit 7 for bytes) as the sign for the number. It will be 1 (set) if the number is negative or 0 (reset) if the number is positive. Your numbers are then 'signed'. It's like they have a sign (plus or minus) inside of them (the sign is represented by the most left bit, the most significant bit).

Signed
Name	Min value	Max value
Nibble	1111 (-8 dec)	0111 (+7 dec)
Byte	1111 1111 (-128 dec)	0111 1111 (+127 dec)
Word	1111 1111 1111 1111 (-32768 dec)	0111 1111 1111 1111 (+32767 dec)

Converting is done by dividing the decimal number by 2 and writing down the remainder. You go on with dividing until everything is gone, while you write down the remainder every time (going from right to left) . You now have the binary equivalent. The picture underneath makes it more clear.

You start at the LSB (Least Significant Bit, that's the one at the very right, bit 0 for a byte) and attribute a value 2^0 to it. Go one bit to the left and give that one the value 2^1. The one on the left of that will get 2^2, etc... Keep doing this until all the bits have an according value.
Then you multiply each bit (that will be '0' or '1') with the according value. You can see an example below.

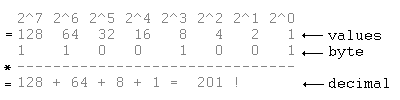
The binary system has some bad points:

When you want to represent big numbers, the list of ones and zeros will get way too long.
Example: Suppose you need to represent the number 65231. In binary, that would give 1111111011001111.

This could lead to mistakes(for example: forgetting a 1 or putting in an extra 0 by accident) and to unreadable sourcecode of programs.

So we are in search of an easier notation, and that will be the hexadecimal notation. We won't throw away all the binary stuff though. Sometimes it will be absolutely necessary to write something in binary instead of in hex. And if we are not talking about memory location, we will mostly keep using the decimal system.

Where the decimal notation has base 10 and the binary notation has base 2, the hexadecimal notation has base 16. To indicate the numbers 10-15 the characters A-F are used. Counting in hex goes like this : 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,10,11,... Take a look at the table that I gave with the binary notations. The third column has the hexadecimal notation.

Converting binary->hexadecimal

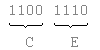Converting a byte to its hexadecimal notation is pretty simple. A byte consists of 2 nbbles, remember? And as each nibble can contain 16 different values (0-15), you can replace each nibble with the hexadecimal equivalent. So 1111 0011 would be F3 in hexadecimal notation.

Converting decimal->hexadecimal

Converting decimal to hexadecimal goes in the same way as converting decimal to binary, but this time you divide by 16 instead of 2 and replace the remainder by the hex equivalent. The remainders are still collected backwards (starting from the right and going to the left side) to get the result.

Converting hexadecimal->decimal

Converting hexadecimal to decimal also goes in the same way as converting binary to decimal, but this time you multiply with the powers of 16 instead of with the powers of 2.

A little table:

Conversions
Dec	Bin	Hex		Dec	Bin	Hex
0	0000	0		8	1000	8
1	0001	1		9	1001	9
2	0010	2		10	1010	A
3	0011	3		11	1011	B
4	0100	4		12	1100	C
5	0101	5		13	1101	D
6	0110	6		14	1110	E
7	0111	7		15	1111	F

To tell other people and the compiler program whether a given number is hex, binary or decimal, you need to add a mark. For example, can you tell me if 1101 is decimal, hexadecimal or binary? I can't!
When you have a hexadecimal number, you add '$' in front or a 'H' on the end, so $3F and 30H are hexadecimal
On binary numbers, you add a '%' in front or a 'b' on the end. Example : %00111111 and 01010000b are binary numbers
On decimal numbers, you add nothing or a 'd' at the end. Example : 1005d is decimal

Notations
Type	Prefix	Suffix
Binary numbers	%11010000	0001000b
Hex numbers	$FF	800Ch
Decimal numbers	10	20d